TEORIA DOS NÚMEROS I
De acordo com Marília Centurión (2002), realizamos uma operação toda vez que agimos sobre os objetos e realizamos neles alguma transformação. Nesse contexto, leia as afirmativas a seguir:
I.O conjunto dos números naturais goza da propriedade de fechamento em relação à adição e a multiplicação
II. Multiplicando uma expressão pelo número 1(um), o resultado não se altera. Assim o elemento neutro da multiplicação é o número 1(um), no conjunto dos números naturais.
III. Na multiplicação, podemos associar dois ou mais fatores pelo seu produto, sem alterar o resultado final.
É correto apenas o que se afirma em:
Apenas I e II
Apenas I e III
Apenas II
I, II e III
Apenas II e III
Determine quantos múltiplos de 6 existem entre 10 e 1 000.
180
155
195
185
165
O produto dos 3° e o 4º termos da sequência a seguir é:

30
-15
15
-30
0
A sequência de triângulos equiláteros, ilustrada na figura, apresenta certo número de pontos assinalados em cada triângulo

Seguindo a lógica utilizada na construção da sequência, o número de pontos que estarão assinalados no décimo triângulo é
45
55
64
54
66
Alguns estudiosos pesquisaram sobre a origem dos números e acabaram percebendo que não os números, mas que a necessidade de contar já existia a cerca de 30.000 anos atrás. Com base nesta afirmativa, avalie as seguintes asserções e a relação proposta entre elas:
I.Se você der a uma criança, que ainda não sabe contar, certa quantidade de bolinhas e em seguida você retirar algumas delas, a criança não perceberá quantas bolinhas foram retiradas, mas saberá que a quantidade foi modificada.
Porque
II.O senso numérico é a capacidade que permite diferenciar, sem contar, se as quantidades foram modificadas, alteradas ou não.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa
As asserções I e II são proposições falsas.
Na locadora Viva Bem cobra 3 reais pela diária de cada DVD alugado. Bruno alugou 5 filmes para assistir durante alguns dias. Analise as alternativas a seguir, na qual apresenta uma afirmação verdadeira sobre o total, em real, pago por Bruno à locadora, independentemente do número de dias de aluguel desses filmes é igual :
O total é múltiplo de 10
O total é múltiplo de 6
O total é múltiplo de 2
O total é múltiplo de 4
O total é múltiplo de 15
Sabemos que os números são resultantes de uma operação de contagem que segue alguns princípios lógicos e possui variadas formas de registro, estabelecendo assim uma relação entre a contagem, a quantificação, os sistemas de registro e os sistemas de numeração. Sendo assim, leia as afirmativas a seguir:
I.Não se pode precisar quando ela iniciou, no entanto acredita-se que os homens primitivos, antes de contar, tinham já um senso numérico que lhes possibilitava identificar mais e menos, poucos e muitos.
II. De certa forma conjectura-se que os homens primitivos eram capazes de reconhecer, numa percepção visual, a variação de quantidades entre conjuntos, a essa variação podemos chamá-la de senso numérico.
III. Com a ampliação da necessidade humama de representar a quantidade, exigia-lhe então pensar mais do que o senso numérico então iniciou-se o processo que hoje chamamos de contagem.
E correto que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.
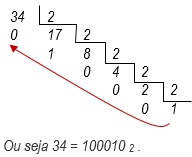
Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:
Apenas I e II
Apenas I e III
Apenas II
I, II e III
Apenas II e III
Determine quantos múltiplos de 6 existem entre 10 e 1 000.
180
155
195
185
165
O produto dos 3° e o 4º termos da sequência a seguir é:

30
-15
15
-30
0
A sequência de triângulos equiláteros, ilustrada na figura, apresenta certo número de pontos assinalados em cada triângulo

Seguindo a lógica utilizada na construção da sequência, o número de pontos que estarão assinalados no décimo triângulo é
45
55
64
54
66
Alguns estudiosos pesquisaram sobre a origem dos números e acabaram percebendo que não os números, mas que a necessidade de contar já existia a cerca de 30.000 anos atrás. Com base nesta afirmativa, avalie as seguintes asserções e a relação proposta entre elas:
I.Se você der a uma criança, que ainda não sabe contar, certa quantidade de bolinhas e em seguida você retirar algumas delas, a criança não perceberá quantas bolinhas foram retiradas, mas saberá que a quantidade foi modificada.
Porque
II.O senso numérico é a capacidade que permite diferenciar, sem contar, se as quantidades foram modificadas, alteradas ou não.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa
As asserções I e II são proposições falsas.
Na locadora Viva Bem cobra 3 reais pela diária de cada DVD alugado. Bruno alugou 5 filmes para assistir durante alguns dias. Analise as alternativas a seguir, na qual apresenta uma afirmação verdadeira sobre o total, em real, pago por Bruno à locadora, independentemente do número de dias de aluguel desses filmes é igual :
O total é múltiplo de 10
O total é múltiplo de 6
O total é múltiplo de 2
O total é múltiplo de 4
O total é múltiplo de 15
Sabemos que os números são resultantes de uma operação de contagem que segue alguns princípios lógicos e possui variadas formas de registro, estabelecendo assim uma relação entre a contagem, a quantificação, os sistemas de registro e os sistemas de numeração. Sendo assim, leia as afirmativas a seguir:
I.Não se pode precisar quando ela iniciou, no entanto acredita-se que os homens primitivos, antes de contar, tinham já um senso numérico que lhes possibilitava identificar mais e menos, poucos e muitos.
II. De certa forma conjectura-se que os homens primitivos eram capazes de reconhecer, numa percepção visual, a variação de quantidades entre conjuntos, a essa variação podemos chamá-la de senso numérico.
III. Com a ampliação da necessidade humama de representar a quantidade, exigia-lhe então pensar mais do que o senso numérico então iniciou-se o processo que hoje chamamos de contagem.
E correto que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.

Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:
180
155
195
185
165
O produto dos 3° e o 4º termos da sequência a seguir é:

30
-15
15
-30
0
A sequência de triângulos equiláteros, ilustrada na figura, apresenta certo número de pontos assinalados em cada triângulo

Seguindo a lógica utilizada na construção da sequência, o número de pontos que estarão assinalados no décimo triângulo é
45
55
64
54
66
Alguns estudiosos pesquisaram sobre a origem dos números e acabaram percebendo que não os números, mas que a necessidade de contar já existia a cerca de 30.000 anos atrás. Com base nesta afirmativa, avalie as seguintes asserções e a relação proposta entre elas:
I.Se você der a uma criança, que ainda não sabe contar, certa quantidade de bolinhas e em seguida você retirar algumas delas, a criança não perceberá quantas bolinhas foram retiradas, mas saberá que a quantidade foi modificada.
Porque
II.O senso numérico é a capacidade que permite diferenciar, sem contar, se as quantidades foram modificadas, alteradas ou não.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa
As asserções I e II são proposições falsas.
Na locadora Viva Bem cobra 3 reais pela diária de cada DVD alugado. Bruno alugou 5 filmes para assistir durante alguns dias. Analise as alternativas a seguir, na qual apresenta uma afirmação verdadeira sobre o total, em real, pago por Bruno à locadora, independentemente do número de dias de aluguel desses filmes é igual :
O total é múltiplo de 10
O total é múltiplo de 6
O total é múltiplo de 2
O total é múltiplo de 4
O total é múltiplo de 15
Sabemos que os números são resultantes de uma operação de contagem que segue alguns princípios lógicos e possui variadas formas de registro, estabelecendo assim uma relação entre a contagem, a quantificação, os sistemas de registro e os sistemas de numeração. Sendo assim, leia as afirmativas a seguir:
I.Não se pode precisar quando ela iniciou, no entanto acredita-se que os homens primitivos, antes de contar, tinham já um senso numérico que lhes possibilitava identificar mais e menos, poucos e muitos.
II. De certa forma conjectura-se que os homens primitivos eram capazes de reconhecer, numa percepção visual, a variação de quantidades entre conjuntos, a essa variação podemos chamá-la de senso numérico.
III. Com a ampliação da necessidade humama de representar a quantidade, exigia-lhe então pensar mais do que o senso numérico então iniciou-se o processo que hoje chamamos de contagem.
E correto que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.

Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:
30
-15
15
-30
0
A sequência de triângulos equiláteros, ilustrada na figura, apresenta certo número de pontos assinalados em cada triângulo

Seguindo a lógica utilizada na construção da sequência, o número de pontos que estarão assinalados no décimo triângulo é
45
55
64
54
66
Alguns estudiosos pesquisaram sobre a origem dos números e acabaram percebendo que não os números, mas que a necessidade de contar já existia a cerca de 30.000 anos atrás. Com base nesta afirmativa, avalie as seguintes asserções e a relação proposta entre elas:
I.Se você der a uma criança, que ainda não sabe contar, certa quantidade de bolinhas e em seguida você retirar algumas delas, a criança não perceberá quantas bolinhas foram retiradas, mas saberá que a quantidade foi modificada.
Porque
II.O senso numérico é a capacidade que permite diferenciar, sem contar, se as quantidades foram modificadas, alteradas ou não.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa
As asserções I e II são proposições falsas.
Na locadora Viva Bem cobra 3 reais pela diária de cada DVD alugado. Bruno alugou 5 filmes para assistir durante alguns dias. Analise as alternativas a seguir, na qual apresenta uma afirmação verdadeira sobre o total, em real, pago por Bruno à locadora, independentemente do número de dias de aluguel desses filmes é igual :
O total é múltiplo de 10
O total é múltiplo de 6
O total é múltiplo de 2
O total é múltiplo de 4
O total é múltiplo de 15
Sabemos que os números são resultantes de uma operação de contagem que segue alguns princípios lógicos e possui variadas formas de registro, estabelecendo assim uma relação entre a contagem, a quantificação, os sistemas de registro e os sistemas de numeração. Sendo assim, leia as afirmativas a seguir:
I.Não se pode precisar quando ela iniciou, no entanto acredita-se que os homens primitivos, antes de contar, tinham já um senso numérico que lhes possibilitava identificar mais e menos, poucos e muitos.
II. De certa forma conjectura-se que os homens primitivos eram capazes de reconhecer, numa percepção visual, a variação de quantidades entre conjuntos, a essa variação podemos chamá-la de senso numérico.
III. Com a ampliação da necessidade humama de representar a quantidade, exigia-lhe então pensar mais do que o senso numérico então iniciou-se o processo que hoje chamamos de contagem.
E correto que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.

Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:
45
55
64
54
66
Alguns estudiosos pesquisaram sobre a origem dos números e acabaram percebendo que não os números, mas que a necessidade de contar já existia a cerca de 30.000 anos atrás. Com base nesta afirmativa, avalie as seguintes asserções e a relação proposta entre elas:
I.Se você der a uma criança, que ainda não sabe contar, certa quantidade de bolinhas e em seguida você retirar algumas delas, a criança não perceberá quantas bolinhas foram retiradas, mas saberá que a quantidade foi modificada.
Porque
II.O senso numérico é a capacidade que permite diferenciar, sem contar, se as quantidades foram modificadas, alteradas ou não.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa
As asserções I e II são proposições falsas.
Na locadora Viva Bem cobra 3 reais pela diária de cada DVD alugado. Bruno alugou 5 filmes para assistir durante alguns dias. Analise as alternativas a seguir, na qual apresenta uma afirmação verdadeira sobre o total, em real, pago por Bruno à locadora, independentemente do número de dias de aluguel desses filmes é igual :
O total é múltiplo de 10
O total é múltiplo de 6
O total é múltiplo de 2
O total é múltiplo de 4
O total é múltiplo de 15
Sabemos que os números são resultantes de uma operação de contagem que segue alguns princípios lógicos e possui variadas formas de registro, estabelecendo assim uma relação entre a contagem, a quantificação, os sistemas de registro e os sistemas de numeração. Sendo assim, leia as afirmativas a seguir:
I.Não se pode precisar quando ela iniciou, no entanto acredita-se que os homens primitivos, antes de contar, tinham já um senso numérico que lhes possibilitava identificar mais e menos, poucos e muitos.
II. De certa forma conjectura-se que os homens primitivos eram capazes de reconhecer, numa percepção visual, a variação de quantidades entre conjuntos, a essa variação podemos chamá-la de senso numérico.
III. Com a ampliação da necessidade humama de representar a quantidade, exigia-lhe então pensar mais do que o senso numérico então iniciou-se o processo que hoje chamamos de contagem.
E correto que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.

Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa
As asserções I e II são proposições falsas.
Na locadora Viva Bem cobra 3 reais pela diária de cada DVD alugado. Bruno alugou 5 filmes para assistir durante alguns dias. Analise as alternativas a seguir, na qual apresenta uma afirmação verdadeira sobre o total, em real, pago por Bruno à locadora, independentemente do número de dias de aluguel desses filmes é igual :
O total é múltiplo de 10
O total é múltiplo de 6
O total é múltiplo de 2
O total é múltiplo de 4
O total é múltiplo de 15
Sabemos que os números são resultantes de uma operação de contagem que segue alguns princípios lógicos e possui variadas formas de registro, estabelecendo assim uma relação entre a contagem, a quantificação, os sistemas de registro e os sistemas de numeração. Sendo assim, leia as afirmativas a seguir:
I.Não se pode precisar quando ela iniciou, no entanto acredita-se que os homens primitivos, antes de contar, tinham já um senso numérico que lhes possibilitava identificar mais e menos, poucos e muitos.
II. De certa forma conjectura-se que os homens primitivos eram capazes de reconhecer, numa percepção visual, a variação de quantidades entre conjuntos, a essa variação podemos chamá-la de senso numérico.
III. Com a ampliação da necessidade humama de representar a quantidade, exigia-lhe então pensar mais do que o senso numérico então iniciou-se o processo que hoje chamamos de contagem.
E correto que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.

Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:
O total é múltiplo de 10
O total é múltiplo de 6
O total é múltiplo de 2
O total é múltiplo de 4
O total é múltiplo de 15
Sabemos que os números são resultantes de uma operação de contagem que segue alguns princípios lógicos e possui variadas formas de registro, estabelecendo assim uma relação entre a contagem, a quantificação, os sistemas de registro e os sistemas de numeração. Sendo assim, leia as afirmativas a seguir:
I.Não se pode precisar quando ela iniciou, no entanto acredita-se que os homens primitivos, antes de contar, tinham já um senso numérico que lhes possibilitava identificar mais e menos, poucos e muitos.
II. De certa forma conjectura-se que os homens primitivos eram capazes de reconhecer, numa percepção visual, a variação de quantidades entre conjuntos, a essa variação podemos chamá-la de senso numérico.
III. Com a ampliação da necessidade humama de representar a quantidade, exigia-lhe então pensar mais do que o senso numérico então iniciou-se o processo que hoje chamamos de contagem.
E correto que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.

Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:
I e II apenas
I e III apenas
II e III apenas
I , II e III
I apenas
Dividimos sucessivamente o número da base decimal por 2 até que não seja mais divisível, ao final, o número binário é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter o número 34 para a base binária.

Seguindo o exposto acima, é correto afirmar que a conversão do número decimal 92 para o número binário é exatamente:
10110100 2
1010100 2
1011100 2
011010 2
101110 2
Ao longo da história, os matemáticos organizaram algumas regras básicas que caracterizam os números naturais e que permitem de forma rápida e acertada, determinar se um número natural é ou não divisível por outro. Essas regras ficaram conhecidas como critérios da divisibilidade.
Sendo assim, leia as afirmativas a seguir:
I. Se n é um múltiplo de a e a ≠ 0, então o resto da divisão de n por a é zero.
II.Se a divisão de n por a tem resto zero, então n é um múltiplo de a.
III. n é um múltiplo de a se, e somente se, a divisão de n por a for exata.
É correto o que se afirma em:

10110100 2
1010100 2
1011100 2
011010 2
101110 2